turtlebot3_slamでcartographerを動かすとき
バージョンはMelodic
基本はgmappingでこれは簡単に動かせる。
以下が見やすい。
あ、geometry2をそのまま持ってくるとrvizが起動できなくなりました。
以下のようなエラーがでる。
$ rviz [ INFO] [1590325929.898961066]: rviz version 1.13.9 [ INFO] [1590325929.899033435]: compiled against Qt version 5.9.5 [ INFO] [1590325929.899054071]: compiled against OGRE version 1.9.0 (Ghadamon) [ INFO] [1590325929.903039046]: Forcing OpenGl version 0. [ INFO] [1590325930.000721555]: Stereo is NOT SUPPORTED [ INFO] [1590325930.000795105]: OpenGl version: 3 (GLSL 1.3). rviz: symbol lookup error: /opt/ros/melodic/lib/libtf.so: undefined symbol: _ZN7tf2_ros17TransformListenerC1ERN3tf210BufferCoreERKN3ros10NodeHandleEb
ブランチを指定します。
$ git clone -b melodic-devel https://github.com/ros/geometry2.git
あとは必要なパッケージをインストールします。
$ sudo apt install ros-melodic-cartographer ros-melodic-cartographer-ros ros-melodic-cartographer-ros-msgs ros-melodic-cartographer-rviz
gazeboで動かす
$ roslaunch turtlebot3_gazebo turtlebot3_world.launch $ roslaunch turtlebot3_teleop turtlebot3_teleop_key.launch
gmappingでなくcartographerで動かしたいときは以下のように実行すればいいのですが、そのまま実行するとエラーがでる。
$ roslaunch turtlebot3_slam turtlebot3_slam.launch slam_methods:=cartographer [ INFO] [1588424028.931538240, 483.493000000]: I0502 21:53:48.000000 3089 map_builder_bridge.cc:130] Added trajectory with ID '0'. F0502 21:53:49.179692 3089 sensor_bridge.cc:126] Check failed: sensor_to_tracking->translation().norm() < 1e-5 The IMU frame must be colocated with the tracking frame. Transforming linear acceleration into the tracking frame will otherwise be imprecise. [FATAL] [1588424029.180452373, 483.544000000]: F0502 21:53:49.000000 3089 sensor_bridge.cc:126] Check failed: sensor_to_tracking->translation().norm() < 1e-5 The IMU frame must be colocated with the tracking frame. Transforming linear acceleration into the tracking frame will otherwise be imprecise.
turtlebot3_lds_2d.luaを編集する。
$ roscd turtlebot3_slam $ gedit config/turtlebot3_lds_2d.lua
tracking_frameをbase_footprintにする。
turtlebot3_lds_2d.lua
-- tracking_frame = "imu_link", tracking_frame = "base_footprint",
これで再度実行すればcartographerができる。
参考
http://emanual.robotis.com/docs/en/platform/turtlebot3/slam/
https://github.com/cartographer-project/cartographer_ros/issues/278
ROSのメモ
環境はWindowsにVirtualBoxでUbuntu18.04
もちろんmelodic
ROSのインストールはroswikiのとおり
そのあとgazeboを起動したらエラーがでた
$ gazebo [Err] [REST.cc:205] Error in REST request
~/.ignition/fuel/config.yamlを編集する。
$ gedit ~/.ignition/fuel/config.yaml
以下の通り
# url: https://api.ignitionfuel.org url: https://api.ignitionrobotics.org
display.launchを起動したらjoint-state-publisher-guiが入ってなかったのでインストール
$ sudo apt install ros-melodic-joint-state-publisher-gui
gazeboの読み込み中のエラー
gzclientまたはgzserverを開いている可能性がある、以下を実行してから再度gazeboを実行するとうまくいく
killall gzserver killall gzclient
ros_controlで、ハードウェア側をVelocityJointInterfaceに設定していると、実行したときに以下のエラーが出る。
実行は成功するので支障はない。
エラーが発生するのは、RobotHWSimを初期化するときにrobot_ros_controlがpid_gainsをロードしようとするためらしい。
[ERROR] [1588774767.409015602, 0.084000000]: No p gain specified for pid. Namespace: /my_robot/gazebo_ros_control/pid_gains/my_joint
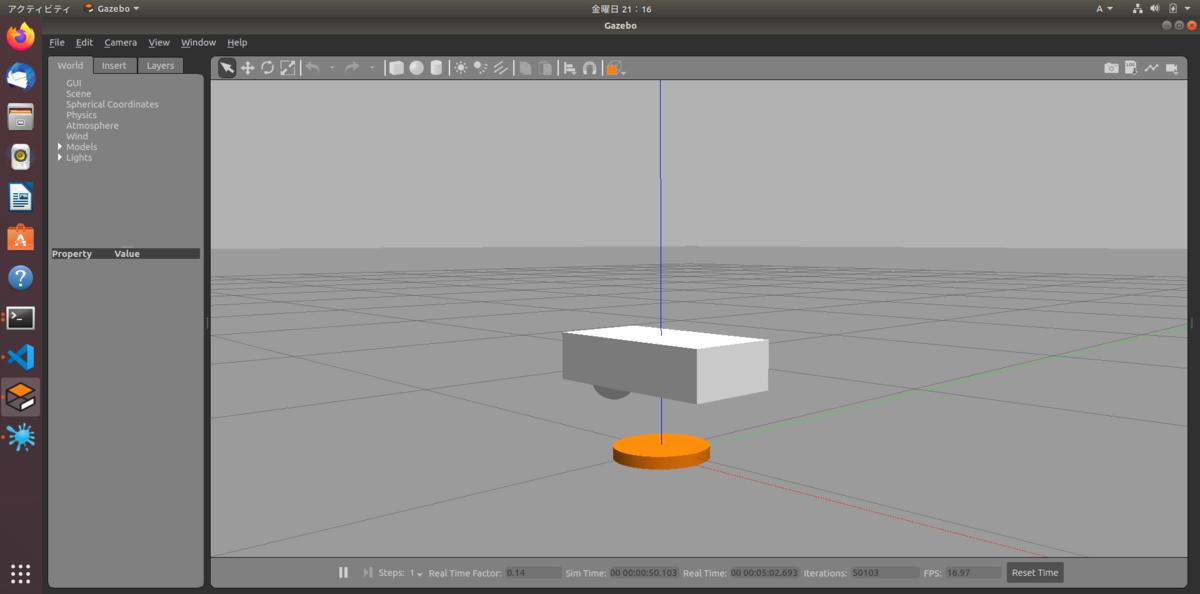
また、EffortJointInterfaceに設定して再度実行、gazeboを起動したら以下のようにバラバラになってしまう。
pidゲインが大きいためらしい。
pidゲインを小さく設定しなおすとなおる。
coppeliarSimをrosで使いたい。
CMakeLists.txtを編集
LIBRARY DESTINATION libを追加
install(TARGETS simExtROSInterface
DESTINATION ${COPPELIASIM_PLUGINS_DIR}
LIBRARY DESTINATION lib
)sudo apt install xsltproc
xacroからsdfへの変換
rosrun xacro xacro --inorder robot.xacro > robot.urdf gz sdf -p robot.urdf > robot.sdf
for i in $(ls /dev/); do $(lsusb -D $i); done
メカナムホイールロボットの可操作性楕円体についてmatlabで描画
Manipulability Ellipsoid of mecanum wheel robot
移動ロボットの可操作性楕円体を求めてみようという試みです。
メカナムロボットの運動学
上図のようなメカナムホイールロボットの運動学は以下の式のようになっています。
詳しく書いているので上のページも参考に。
以下の式のような形になっていることがわかります。
ここで、式変形して以下のような形にしたとき、J(θ)をヤコビ行列と呼びます。
ロボットアームなどでは、ヤコビ行列から可操作性楕円体を求めて、そのロボットアームのある姿勢における操作性(動かしやすさ)を評価することがあります。
今回はメカナムホイールロボットの可操作性楕円体を求めます。
ただし、回転に関する操作性は考慮しないため、使用する式を以下のように変えます。
に関する式を取り除きます。
コード
コードはmatlabで書きました。
fai = deg2rad(30); % メカナムホイールのローラの傾き theta = deg2rad(10); % 絶対座標に対するロボット本体の傾き A = [-sin(fai) cos(fai); -sin(fai) -cos(fai); sin(fai) -cos(fai);sin(fai) cos(fai)]; R = [cos(theta) sin(theta); -sin(theta) cos(theta)]; J = inv(R) * pinv(A); % 可操作性楕円体の描画 figure(1); X = 0; Y = 0; drawManipulabilityEllipsoid(X, Y, J); hold on; % ロボットの描画 b_wh= 0.2; % 車輪の幅 d_wh = 0.3; % 車輪の直径 r_a = 0.5; % 機体の幅 robot_shape = polyshape([-r_a/2 -r_a/2 r_a/2 r_a/2],[r_a/2 -r_a/2 -r_a/2 r_a/2]); wheel1_x = [r_a/2 r_a/2 r_a/2+b_wh r_a/2+b_wh]; wheel1_y = [r_a/2+d_wh/2 r_a/2-d_wh/2 r_a/2-d_wh/2 r_a/2+d_wh/2]; wheel1_shape = polyshape(wheel1_x, wheel1_y); wheel2_shape = polyshape(-wheel1_x, wheel1_y); wheel3_shape = polyshape(-wheel1_x, -wheel1_y); wheel4_shape = polyshape(wheel1_x, -wheel1_y); robot_pose = rotate(robot_shape, rad2deg(theta)); wheel_pose = rotate([wheel1_shape wheel2_shape wheel3_shape wheel4_shape], rad2deg(theta)); plot(robot_pose, 'FaceColor', 'w'); plot(wheel_pose, 'FaceColor', 'b'); quiver(0,0,0.5*cos(theta),0.5*sin(theta), 'Color', 'k', 'LineWidth', 3, 'MaxHeadSize', 3); quiver(0,0,0.5*cos(theta+pi/2),0.5*sin(theta+pi/2), 'Color', 'k', 'LineWidth', 3, 'MaxHeadSize', 3); text(0.5*cos(theta),0.5*sin(theta),'X_R','FontSize',20); text(0.5*cos(theta+pi/2),0.5*sin(theta+pi/2),'Y_R','FontSize',20); axis equal; grid on;
楕円を描画する関数
function drawManipulabilityEllipsoid(X, Y, J) % 可操作性楕円体のための行列をヤコビ行列から作成 A = J*J.'; [V,D] = eig(A); % 固有値^(1/2)を取得 Lambda = [D(1,1)^0.5,D(2,2)^0.5]; Lambda_1 = Lambda(1); Lambda_2 = Lambda(2); % 固有ベクトル V_1 = V(:,1); V_2 = V(:,2); N = 200; % 固有値から楕円の大きさを取得 a = Lambda_2; b = Lambda_1; x = zeros(1,4*N); y = zeros(1,4*N); for i = 1:2*N t = a-a/N*(i-1); x(i) = t; y(i) = b*(1-t^2/a^2)^0.5; end for i = 1:2*N t = -a+a/N*(i-1); x(2*N+i) = t; y(2*N+i) = -b*(1-t^2/a^2)^0.5; end x(end+1) = x(1); y(end+1) = y(1); Th_Z = atan2(V(2,2),V(1,2)); rotZ = [cos(Th_Z),-sin(Th_Z);sin(Th_Z),cos(Th_Z)]; ElipXY = rotZ*[x;y]; plot(Lambda_1*[V_1(1), -V_1(1)]+X,Lambda_1*[V_1(2), -V_1(2)]+Y,'m','Linewidth',1.5); plot(Lambda_2*[V_2(1), -V_2(1)]+X,Lambda_2*[V_2(2), -V_2(2)]+Y,'m','Linewidth',1.5); plot(ElipXY(1,:)+X,ElipXY(2,:)+Y,'r','Linewidth',2); end
結果と考察に問題点
実行結果です。
x軸方向に楕円が大きいため、横に動きやすいという結果となりました。
よく考えるとこれはおかしい結果です。
と設定しているため、本当はy軸方向に動きやすいはずです。(ページ最上部の図を見ればわかりやすいと思います)
式やコードが間違っている可能性もありますし、検証したいところです。

てこクランク機構の運動学とpythonでシミュレーション
てこクランク
てこクランク機構は4節リンクの1つです。
1つの原動節の回転から、1つの従動節の揺動運動に変換します。
ここで、固定節を支点としたてこによって従動節の先端の動作が拡大されます。

順運動学
パラメータの設定
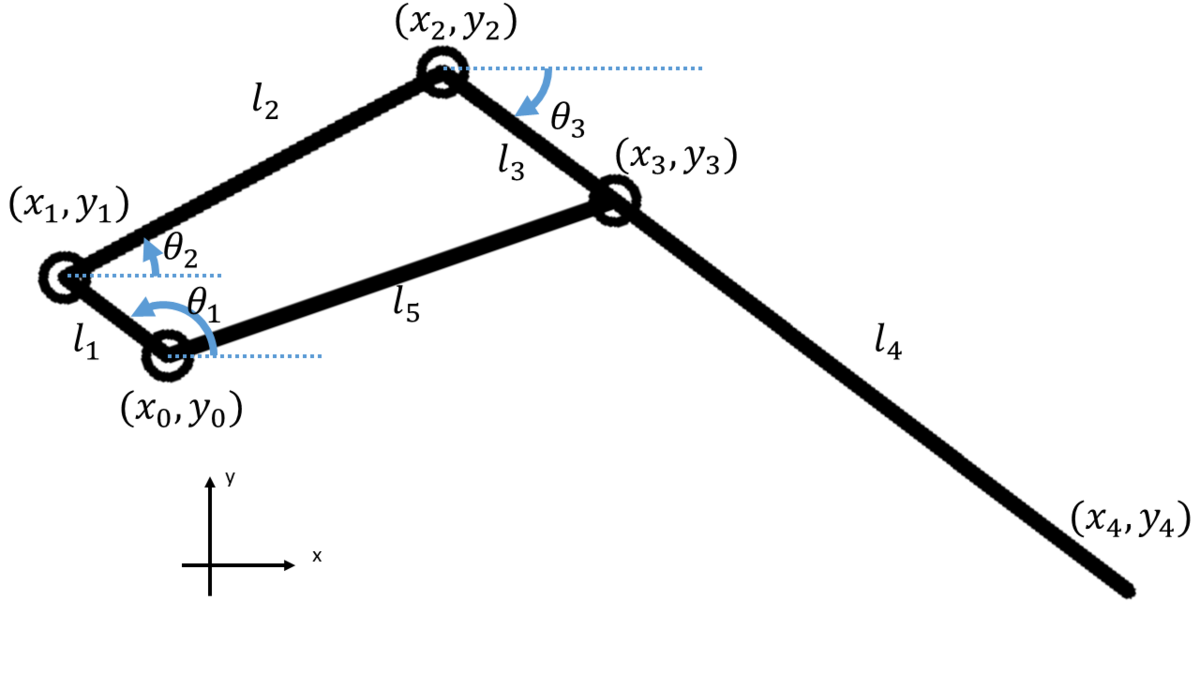
下図のように各リンクの長さ、各節点の座標、角度を設定します。
また、(x0, y0)および(x3, y3)は最初に決めておく既知の値です。
例えば (x3, y3) = (x0+l5, y0) とすれば固定節はx軸に平行になります。
導出
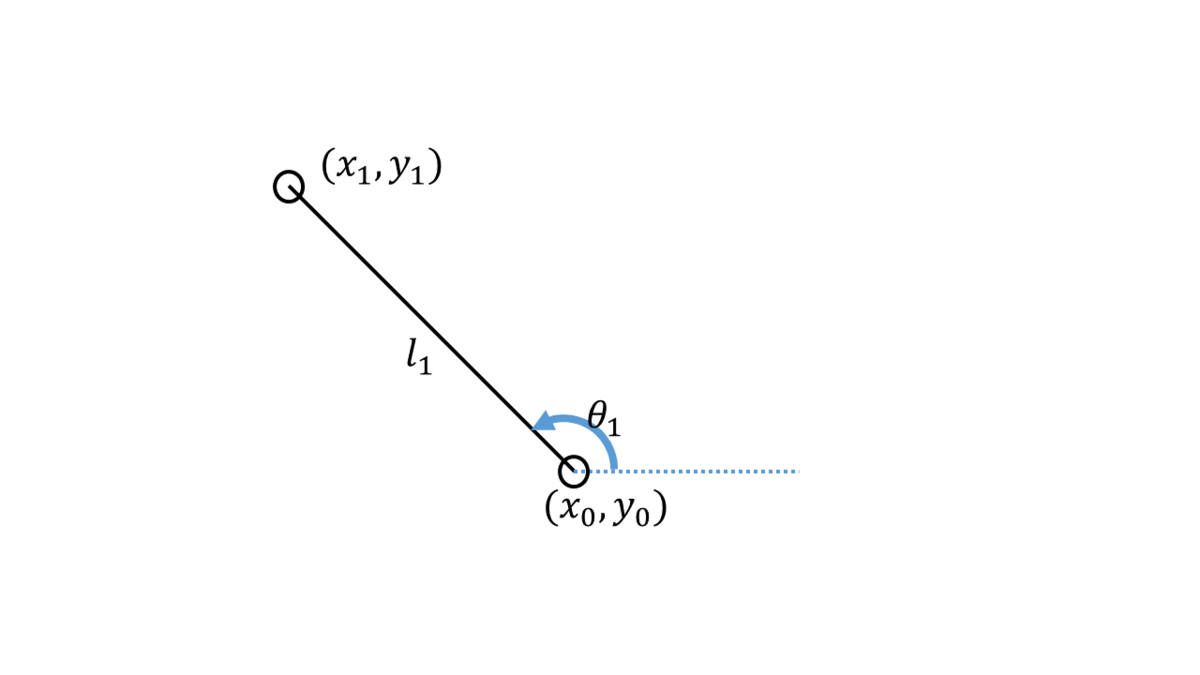
まずは(x1, y1)を求めます。
上図を考えれば、三角関数により簡単に求められます。

次はθ2を求めます。
上図のような三角形を考えると、角度αについての余弦定理から以下の式が成り立ちます。
ただし、Lは以下の長さです。
角度βについても以下の式が成り立ちます。
角度αとβがそれぞれ求まるので、その和によってθ2が求まります。
θ2が求まれば、(x2, y2)も簡単に求まります。

最後に先端座標を求めます。
(x3, y3)が既知で、(x2, y2)が求まっているので、簡単にθ3を求めることができます。
よって先端座標(x4, y4)は以下の式のとおり求まります。
シミュレーション
順運動学が求まりましたが、正しい保証がありません。
求めた式を使ってリンクのシミュレーションを行い、動作が怪しくなければ正しい式といえるでしょう。
シミュレーションはpythonで行います。描画はOpenCVです。
以下のコードを実行するとシミュレーション結果を確認できます。
以下のようにトラックバーによってθ1を操作することができます。

動作の様子です。(先端座標の表示を追加しています。)

import cv2 import numpy as np from math import * SIMULATOR_WINDOW_NAME = 'link simulator' FRAME_WIDTH = 10 NODE_RADIUS = 15 NODE_WIDTH = 5 FRAME_COLOR = (0, 0, 0) POSE_TO_PXL = 0.3 class Frame: def __init__(self, frame_length, frame_width=FRAME_WIDTH, x0=0, y0=0, rad=0, window_name=SIMULATOR_WINDOW_NAME): self.length = frame_length self.x0 = x0 self.y0 = y0 self.rad = rad self.x1 = self.x0 + self.length * cos(self.rad) self.y1 = self.y0 + self.length * sin(self.rad) self.window_name = window_name self.frame_width = frame_width def set_position(self, x0, y0, rad): self.x0 = x0 self.y0 = y0 self.rad = rad self.x1 = self.x0 + self.length * cos(self.rad) self.y1 = self.y0 + self.length * sin(self.rad) def get_EndPosition(self): return self.x1, self.y1 def drawFrame(self, img): if len(img.shape) == 3: self.Height, self.Width, self.channels = img.shape[:3] else: self.Height, self.Width = img.shape[:2] px0 = int(self.x0 * POSE_TO_PXL) py0 = self.Height - int(self.y0 * POSE_TO_PXL) px1 = int(self.x1 * POSE_TO_PXL) py1 = self.Height - int(self.y1 * POSE_TO_PXL) cv2.line(img, (px0,py0), (px1,py1), FRAME_COLOR, self.frame_width) cv2.circle(img, (px0,py0), NODE_RADIUS, FRAME_COLOR, NODE_WIDTH) if __name__ == '__main__': controlBox = np.zeros((300,512,3), np.uint8) cv2.namedWindow('panel') cv2.createTrackbar('deg', 'panel', 0, 1080, lambda x: None) l1 = 300 l2 = 1000 l3 = 500 l4 = 1500 l5 = 1100 f1 = Frame(l1) f2 = Frame(l2) f3 = Frame(l3) f4 = Frame(l4) f5 = Frame(l5) img = np.zeros((600,1000,3), np.uint8) img[:,:,:] = 255 while True: img = np.zeros((600,1000,3), np.uint8) img[:,:,:] = 255 # 順運動学 deg = cv2.getTrackbarPos('deg', 'panel') # θ1はトラックバーから操作 (x0, y0) = (400, 1500) x3, y3 = x0+l5, y0 f1.set_position(x0, y0, deg*pi/180) (x1, y1) = f1.get_EndPosition() L = sqrt( (x3-x1)**2 + (y3-y1)**2 ) theta2 = acos( (l2**2 + L**2 - l3**2) / (2*l2*L) ) + atan2(y3-y1, x3-x1) f2.set_position(x1, y1, theta2) (x2, y2) = f2.get_EndPosition() theta3 = atan2(y3-y2, x3-x2) f3.set_position(x2, y2, theta3) f4.set_position(x3, y3, theta3) x4, y4 = f4.get_EndPosition() f5.set_position(x0, y0, atan2(y3-y0, x3-x0) ) f1.drawFrame(img) f2.drawFrame(img) f3.drawFrame(img) f4.drawFrame(img) f5.drawFrame(img) cv2.imshow(SIMULATOR_WINDOW_NAME, img) if cv2.waitKey(1) > 0: break cv2.destroyAllWindows()
旋盤で穴にキー溝加工をする
軸にキー溝加工をしたかったらフライス盤を使えばよいのですが、穴に溝加工をするとなるとスロッターが必要です。
大学や高専なら汎用フライス盤はあるでしょうが、スロッターが置いてあるところはなかなかないと思います。
ここでは旋盤で穴にキー溝を加工する方法を説明します。
ツールの作成
まずは溝加工をするための工具を製作します。
折れたエンドミルやドリルなどをグラインダで削って以下のような工具を作ります。
先端の幅をキー溝の幅と合わせます。

セッティング
エンドミルの外形に合わせ丸棒の軸方向に穴を開け、先ほどのツールを挿し込みます。
これを旋盤の刃物台にセットします。
ツールが材料の中心と合うように調整してください。
材料はチャックにセットします。
旋盤の回転数は最低速にしておきます(材料が回転してずれるのを防止するため)。
以下はセットの様子です。少し斜めにして刃物台を固定します。


加工
あとは縦方向(半径方向)に少しずつ(0.02~0.05 mmステップ)進めて、刃物台を軸方向に送って削っていきます。
加工の様子です。

以下は実際に加工したカップリングです。
良い精度は出ませんがキーを通したいだけなら十分です。

6軸ジャイロセンサMPU6050をArduinoで使って角度を取得
amazonでなんか安いMPU6050使用のジャイロセンサを使うだけです。
5個セット。お得か?
接続
(MPU6050 - Arduino UNO)
VCC - 5V
GND - GND
SCL - A5
SDA - A4
ライブラリがあるのでこれ使えば簡単です。

以下簡単に3軸の角度を取得するためのサンプルコード
#include "I2Cdev.h" #include "MPU6050.h" #include "Wire.h" MPU6050 accelgyro; int16_t ax, ay, az; int16_t gx, gy, gz; void setup() { Wire.begin(); Serial.begin(38400); // 初期化 accelgyro.initialize(); delay(10); // 計測範囲を2000 deg/secに設定、16.4 LSB/deg/s accelgyro.setFullScaleGyroRange(MPU6050_GYRO_FS_2000); delay(10); accelgyro.CalibrateGyro(); accelgyro.CalibrateAccel(); } void loop() { // 時間を計っとく static float timer = 0; // 各軸加速度と角速度を取得 accelgyro.getMotion6(&ax, &ay, &az, &gx, &gy, &gz); //X、Y軸まわりの角度を計算 float degY = atan2(ax, az) * RAD_TO_DEG; float degX = atan2(ay, az) * RAD_TO_DEG; // Z軸まわりの角度を計算 static float degZ = 0; static int last_time = micros(); float omega = float(gz)/16.4; //omega[deg/s] = gz[LSB] / 16.4[LSB/deg/s] int current_time = micros(); //time[us] float dt = current_time - last_time; // 角度は角速度の積分 degZ += omega *dt/1000000.0; //degZ[deg] = omega[deg/s] * dt[us] / 1000000[us/s] last_time = current_time; Serial.print(timer+=dt/1000000); Serial.print(", "); Serial.print(degX); Serial.print(", "); Serial.print(degY);Serial.print(", "); Serial.println(degZ); }
単方向ブラシレスESCをむりやり双方向にする
ブラシレスESCについて
ブラシレスESCには双方向(bidirectional)のものと片方向のみ制御できるものがあります。
双方向可能なものであればプログラミングカードなどで設定すればよいのですが。
単方向のみのものがあるので、これを使ってどうにかブラシレスモータを双方向に回転させたいのでした。
双方向化のために
双方向のESCを追加で購入するのもなんだし、今あるESCでなんとか双方向制御したい。
ここで、ブラシレスモータ(3相交流モータ)は3本ある線(U, V, W)のうちどれでも2本の線を入れ替えると回転方向が逆になる性質に注目しますと、
電子スイッチで2本の出力を入れ替えてやり回転方向を切り替えるという発想にいたりました。
悲しいね。
実際に作ったもの
これが実際に作った基板です。

- ESC_logicをブラシレスESCと接続
- 右上のXAコネクタVgsに16V程度接続(ゲートドライブ用)。
- Vin、Win(左側の太線)をESCの出力と接続、Vout、Wout(右側の太線)をブラシレスモータの入力と接続
- U相については直接ESCからブラシレスモータに接続します。
- 4ピンXAコネクタ
- GND 制御用マイコンのGNDと接続
- DIR 方向制御用入力(Low:正転、High:逆転)
- RC ESCへのRC入力(PWMね)
- NC 使用しない
- LED
DIRピンの状態によって切り替わります。Highのとき上、Lowのとき下のLEDが点灯します。
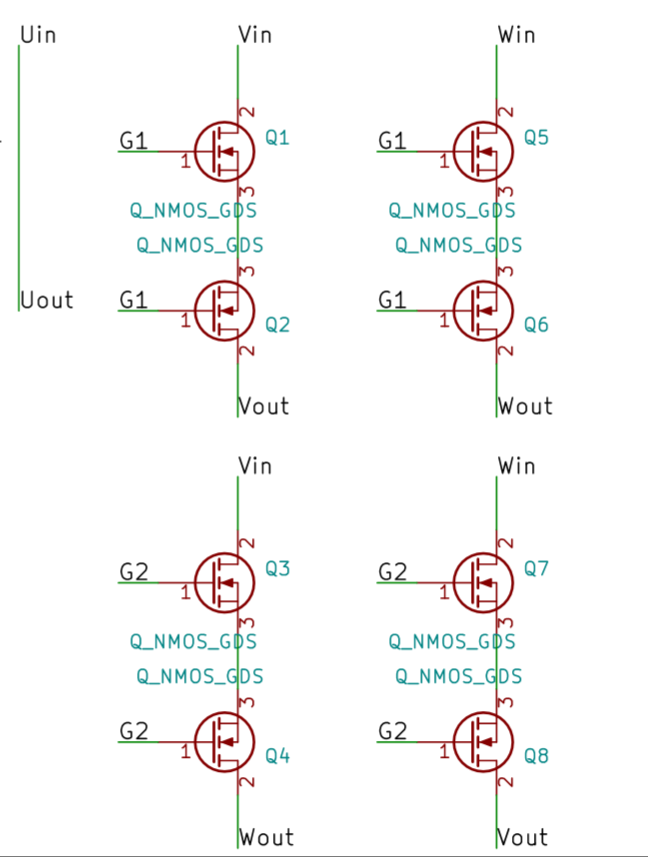
回路
Vin, WinをそれぞれVout, Woutのどちらかに入れ変える回路です。FETで切り替えてます。
DIRピンのON/OFFで2つのフォトカプラの出力(G1, G2)が入れ替わります。

使用部品
FET:PSMN1R5-30YLC
フォトカプラ:TLP621GB-1
トランジスタ:2SC1815
なんで1つの信号(例えばVinからVoutまで)にFET2つ使ってるのかというと、FET内部のダイオードをキャンセルするためです。
1つだとゲートが閉じていてもソースからドレインの方向の信号を止めることができませんでした。
この対処方法が最適かはどうでしょうね。
まとめ
双方向ESCを買いましょう
