メカナムホイールロボットの制御 - 元高専生のロボット作り

メカナムホイール4輪ロボットの制御をしました。

運動学を求める

メカナムホイールロボットを以下の図のようにします。

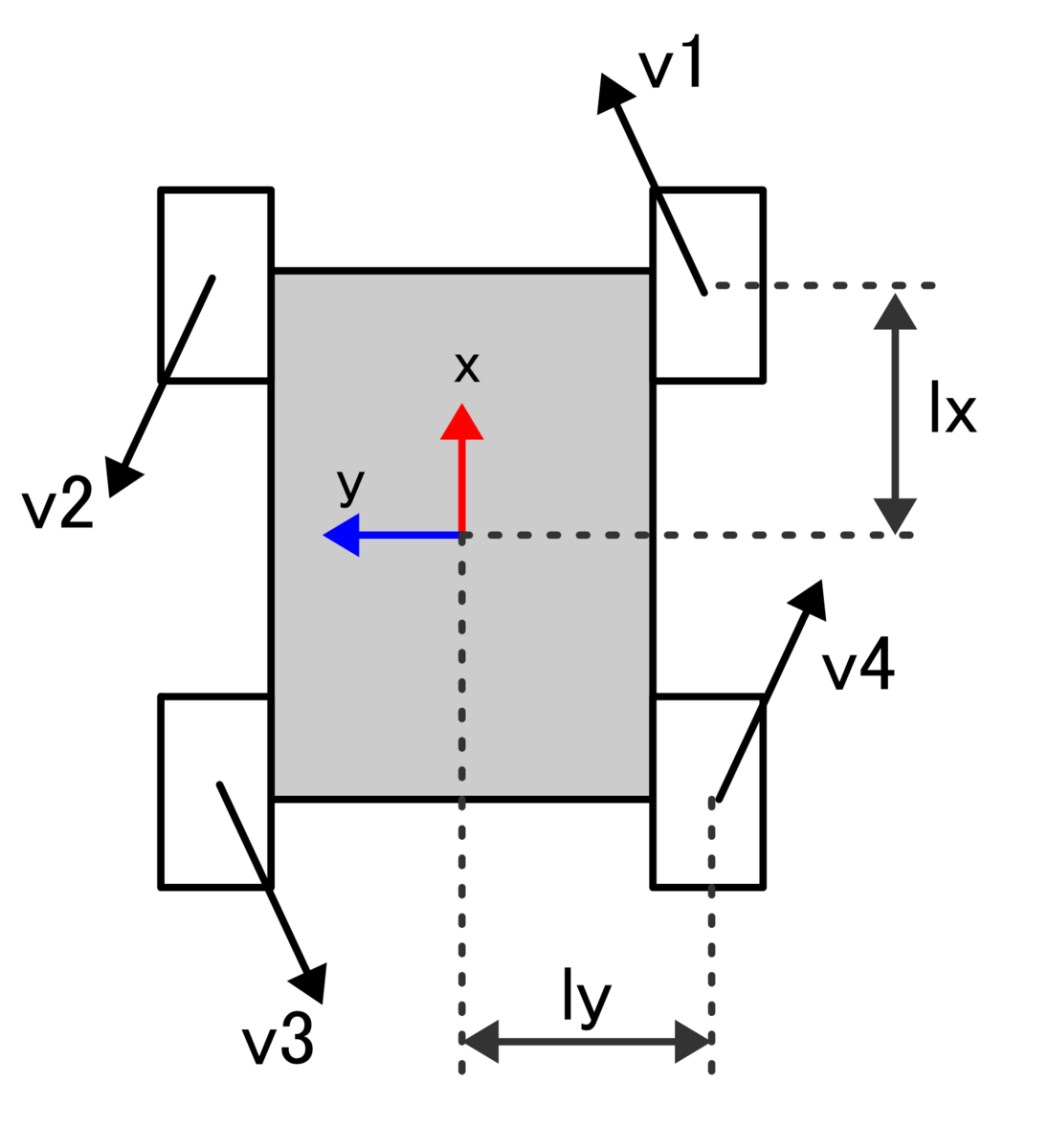
ホイールの角度は基本的に45°であるため，角車輪のx軸とy軸に対する速度の寄与は同じになります．
図より、各ホイールの周速度 $v_1, v_2, v_3, v_4$ とすれば、

$\begin{equation} \begin{aligned} & \mathrm{v}_1=\mathrm{v}_{\mathrm{x}}+\mathrm{v}_{\mathrm{y}}+\left(l_x+l_y\right) \omega \\ & \mathrm{v}_2=-\mathrm{v}_{\mathrm{x}}+\mathrm{v}_{\mathrm{y}}+\left(l_x+l_y\right) \omega \\ & \mathrm{v}_3=-\mathrm{v}_{\mathrm{x}}-\mathrm{v}_{\mathrm{y}}+\left(l_x+l_y\right) \omega \\ & \mathrm{v}_4=\mathrm{v}_{\mathrm{x}}-\mathrm{v}_{\mathrm{y}}+\left(l_x+l_y\right) \omega \end{aligned} \end{equation}$

と求まります。

行列表示すると以下のようになります。

ただし、速度ベクトル $[{\dot { x } } , { \dot { y } } , { \dot { \theta } }$ ] はロボットフレーム{ R }から見た速度です。

実際に制御するときには慣性フレーム{ I }から見たらどう動けばいいのかを考えたいです。
ロボットフレームでの速度ベクトルは、慣性フレームでの速度ベクトルから以下の式で表されます。

$\begin{bmatrix}{ \dot { x } } \\ { \dot { y } } \\ { \dot { \theta } }\end{bmatrix} = \begin{bmatrix} { \cos \theta } & { \sin \theta } & { 0 } \\ { - \sin \theta } & { \cos \theta } & { 0 } \\ { 0 } & { 0 } & { 1 } \end{bmatrix} \begin{bmatrix} { \dot { x } _ { I } } \\ { \dot { y } _ { I } } \\ { \dot { \theta } _ { I } } \end{bmatrix}$

よって、前の式に代入して、以下の式が得られます。

$\begin{bmatrix} { v _ { 1 } } \\ { v _ { 2 } } \\ { v _ { 3 } } \\ { v _ { 4 } } \end{bmatrix} = \begin{bmatrix}{ 1 } & { 1 } & { l_x + l_y } \\ { -1 } & { 1 } & { l_x + l_y } \\ { -1 } & { -1 } & { l_x + l_y } \\ { 1 } & { -1 } & { l_x + l_y } \end{bmatrix} \begin{bmatrix} { \cos \theta } & { \sin \theta } & { 0 } \\ { - \sin \theta } & { \cos \theta } & { 0 } \\ { 0 } & { 0 } & { 1 } \end{bmatrix} \begin{bmatrix}{ \dot { x } _ { l } } \\ { \dot { y } _ { I } } \\ { \dot { \theta } _ { I } } \end{bmatrix}$

これが運動学になります。
この式を用いればロボットの速度及び角速度から、各車輪の速度が求められます。

さて、運動学が求まったのでロボットを制御することができます。

とりあえず、制御データの受け渡しブロック図でも書いてみます。

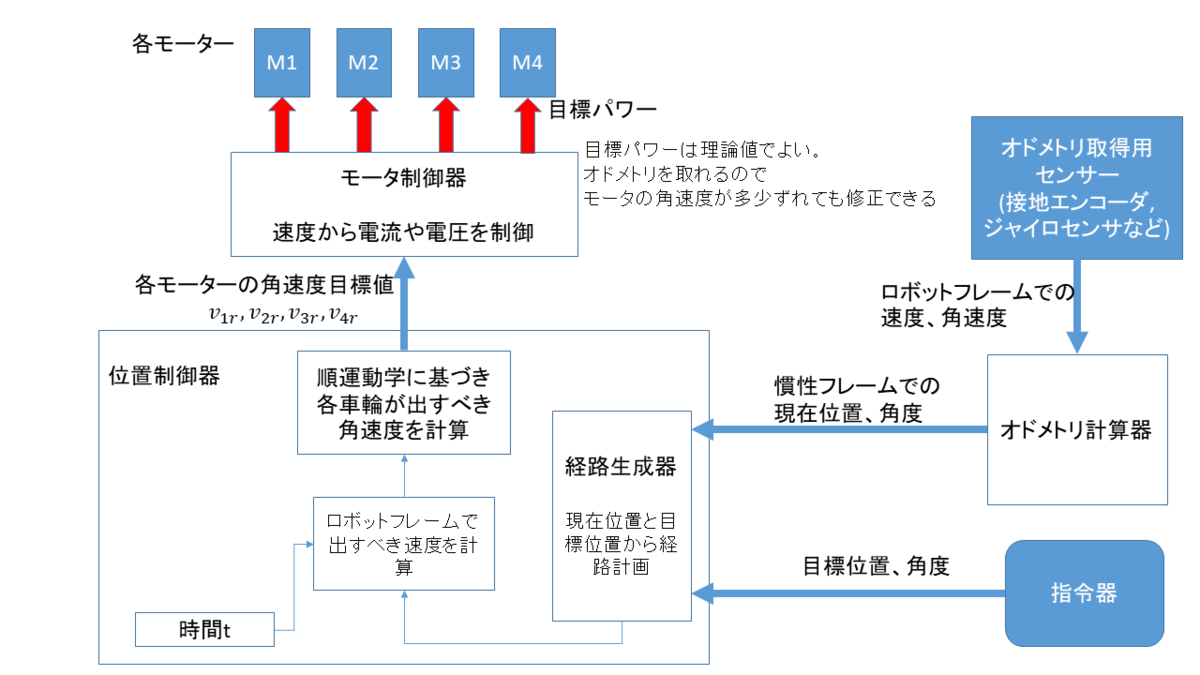
だいたいこんなもんですかね。経路計画のところが若干フワフワしてますね。
簡単に目標位置と現在位置の差分を分割してやればいいんじゃないかな。

つづきはまた今度

おまけ　ついでに順？運動学を求める

普通はオドメトリ用の車輪を別に用意したりするのですが、
車輪の滑りがないという仮定をすれば、各車輪の角速度からロボットの速度が求められます。

ここで簡単のため係数行列を $A$ とおきます。

$\begin{bmatrix} { v _ { 1 } } \\ { v _ { 2 } } \\ { v _ { 3 } } \\ { v _ { 4 } } \end{bmatrix} = A \begin{bmatrix} { \dot { x } } \\ { \dot { y } } \\ { \dot { \theta } } \end{bmatrix}$

運動学を求めるには、係数行列 $A$ の逆行列を求めればよいです。
逆行列 $X$ が求まれば、
$\begin{bmatrix}{ \dot { x } } \\ { \dot { y } } \\ { \dot { \theta } } \end{bmatrix} = X \begin{bmatrix} { v _ { 1 } } \\ { v _ { 2 } } \\ { v _ { 3 } } \\ { v _ { 4 } } \end{bmatrix}$
のように運動学が求まります。

しかし、求めた係数行列 $A$ は4×3行列であるため、疑似逆行列（一般逆行列）というものを用います。
$A$ に対して疑似逆行列は以下の式で求まります。
$A ^ { + } = \left( A ^ { T } A \right) ^ { - 1 } A ^ { T }$

手計算で求めるのは大変なので私はmatlabを使いました。（手計算してもいい）
使用したmatlabコードです。

% φをxとおいた

syms lx ly;
A = [1 1 lx+ly; -1 1 lx+ly; -1 -1 lx+ly; 1 -1 lx+ly];
pinv(A)

出力が以下のように出るので、

ans =
 
[            1/4,            -1/4,            -1/4,             1/4]
[            1/4,             1/4,            -1/4,            -1/4]
[1/(4*(lx + ly)), 1/(4*(lx + ly)), 1/(4*(lx + ly)), 1/(4*(lx + ly))]

求まった疑似逆行列 $A ^ { + }$ を用いて、

$\begin{bmatrix} { \dot { x } } \\ { \dot { y } } \\ { \dot { \theta } } \end{bmatrix} = \frac{1}{4} \begin{bmatrix} { 1 } & { -1 } & { -1 } & { 1 } \\ { 1 } & { 1 } & { -1 } & { -1 } \\ { \frac { 1 } { l_x+l_y } } & { \frac { 1 } { l_x+l_y } } & { \frac { 1 } { l_x+l_y } } & { \frac { 1 } { l_x+l_y } } \end{bmatrix} \begin{bmatrix} { v _ { 1 } } \\ { v _ { 2 } } \\ { v _ { 3 } } \\ { v _ { 4 } } \end{bmatrix}$

と求まります。
これが各車輪の角速度からロボットの速度を求める運動学になります。

運動学を求める

おまけ ついでに順？運動学を求める

おまけ　ついでに順？運動学を求める